Find dy/dx x^2yxy^2=6 Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps By the Sum Rule, the derivative of with respect to is Evaluate Tap for more steps Differentiate using the Product Rule which states that is where andDifferential equation Solve $(2xy^4e^y 2xy^3 y)dx (x^2y^4e^y x^2y^2 3x) dy = 0$ written 51 years ago by aksh_31 ♦ 22k • modified 51 years ago Mumbai University > First Year Engineering > sem 2 > Applied Maths 2 Marks 6 Year 13 applied mathematics ADD COMMENT FOLLOW SHAREFactor out the Greatest Common Factor (GCF), 'dx 2 ' dx 2 (y 2 2x) = 0 Subproblem 1 Set the factor 'dx 2 ' equal to zero and attempt to solve Simplifying dx 2 = 0 Solving dx 2 = 0 Move all terms containing d to the left, all other terms to the right

最新 Xy1 試す
Y xy 2x 2y 2 dx x xyx- 2y 2 dy 0
Y xy 2x 2y 2 dx x xyx- 2y 2 dy 0-Factor out the Greatest Common Factor (GCF), 'dx' dx(3 4y 2xy 2 2x 3) = 0 Subproblem 1 Set the factor 'dx' equal to zero and attempt to solve Simplifying dx = 0 Solving dx = 0 Move all terms containing d to the left, all other terms to the right Simplifying dx = 0 The solution to this equation could not be determinedOther Math questions and answers;




Lesson 6 Exact Equations Determine Whether Or Not Each Of
Factor out the Greatest Common Factor (GCF), 'dxy 2 ' dxy 2 (y 2x) = 0 Subproblem 1 Set the factor 'dxy 2 ' equal to zero and attempt to solve Simplifying dxy 2 = 0 Solving dxy 2 = 0 Move all terms containing d to the left, all other terms to the right So, the given differential equation is exact On integrating M wrt x, treating y as a constant, On integrating N wrt y, treating x as a constant, (omitting 2xy2 2x2y which already occur in ∫M dx) Therefore, the solution of the given equation is x3/3 2x2y 2xy2 y3/3 = λ ⇒ x3 y3 6xy (x y) = 3λFor the differential equation `(x^2y^2)dx2xy dy=0`, which of the following are true (A) solution is `x^2y^2=cx` (B) `x^2y^2=cx` `x^2y^2=xc` (D) `y
Question (2xy^22y)dx(2x^2y2x)dy=0 This problem has been solved!Simple and best practice solution for (xy2xy2)dx (x^22x)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itMathy^2 x^2 (\dfrac{dy}{dx}) = xy(\dfrac{dy}{dx})/math math\dfrac{y}{x} \dfrac{x}{y}(\dfrac{dy}{dx}) = (\dfrac{dy}{dx})/math math\dfrac{y}{x} (\dfrac
Use the distributive property to multiply x 2 y 3 d x d by y To find the opposite of x^ {2}dy^ {4}xdy, find the opposite of each term To find the opposite of x 2 d y 4 x d y, find the opposite of each term Combine ydx and xdy to get 2ydx Combine − y d x and − x d y to get − 2 y d xThe issue is that you integrated y with respect to x, and concluded that it was equal to y This is only viable if y = aex for some constant a, which we have no reason to suspect Solve y ^2x (\frac {dy} {dx})^2 = 1 using proposed change of variables Solve y2 −x(dxdy )2 = 1 using proposed change of variablesRewrite 2xy dxx2 dy−1 dy = 0 2 x y d x x 2 d y − 1 d y = 0 Change the sides $$2 xy \ dx x^2 \ dy = 1 \ See full answer below




Dy Dx 2xy F X Y 0 2 Novocom Top




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history$(xy^22x^2y^3)dx(x^2yx^3y^2)dy=0$ $xy(y2xy^2)dxxy(xx^2y)dy=0$ $f(x,y)=xy(y2xy^2)$ $g(x,y)=xy(xx^2y)$ Here, xy is a common term for both, f(x,y) and g(x,y)It is homogeneous equation




Math 432 Hw 2 4 Solutions Frostburg
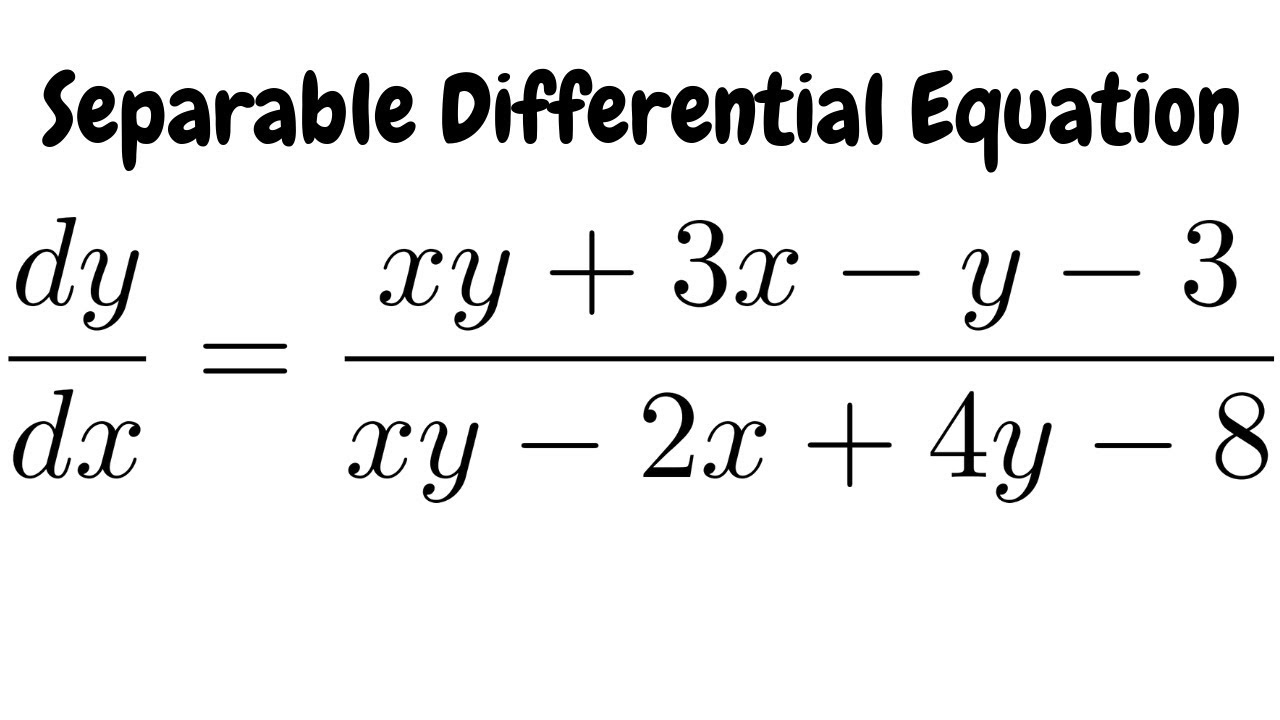



Separable Differential Equation Dy Dx Xy 3x Y 3 Xy 2x 4y 8 Youtube
Solve the differential equation `xy dy/dx = x^2 2y^2` by integrating the side attached to dx with respect to x x^5/5 x^2y^2xy^4k(y) this k represent function of y as you differentiated x you removed y as it wads constant with respect to x this is F(x,y) so you have to diferentiate it with respect to y in order to find k(y) 2xy^24xy^3k'(y) you equal it with the side attached to dy in theSolve the following differential equations 1 (xy 1)dx x(x 4y 2)dy = 0 6 (x y 1)dx (2x 2y 1)dy = 0 2



Bernoulli S Equation 6y 2 Dx X 2x 3 Y Dy 0 Chegg Com




4 Solve The Exact Differential Equation 1 2xy Dx 4y3 X2 Dy 0 4 Solve The Exact Differential Equation Homeworklib
I'm at the beggining of a differential equations course, and I'm stuck solving this equation $$(x^2y^2)dx2xy\ dy=0$$ I'm asked to solve it using 2 different methods I proved I can find integrating factors of type $\mu_1(x)$ and $\mu_2(y/x)$If I'm not wrong, these two integrating factors are $$\mu_1(x)=x^{2} \ \ , \ \ \mu_2(y/x)=\left(1\frac{y^2}{x^2}\right)^{Steps for Solving Linear Equation ( x y ^ { 2 } x ) d x ( y x ^ { 2 } y ) d y = 0 ( x y 2 x) d x ( y x 2 y) d y = 0 Use the distributive property to multiply xy^ {2}x by d Use the distributive property to multiply x y 2 x by d \left (xy^ {2}dxd\right)x\left (yx^ {2}y\right)dy=0Click here👆to get an answer to your question ️ Solution of the differential equation y(xy 2x^2y^2)dx x(xy x^2y^2)dy = 0 is given by plogx Qlogy 1/xy = C




Xy X 2y 1 0 Novocom Top




Solve The Differential Equation X Y 2 X Dx Y X 2 Y Dy 0
Solve $(2x^2 y^2)\,dx xy \, dy = 0$ Attempted The equation is not exact because $ M_y \ne N_x $ for $ M = 2x^2 y^2 $ and $ N = xy$ Or is it exact? The solution of the differential equation (3xy y^2)dx (x^2 xy)dy = 0 is (A) x^2(2xy y^2) = c^2 asked in Differential equations by AmanYadav ( 556k points) differential equations1 Answer1 Active Oldest Votes 1 The solution (below) is obtained on the form of an implicit equation Then, it is not very difficult to explicit x ( y) But it seems not possible to get a closed form for the inverse function y ( x) with the available standard functions Share answered Dec 16 '16 at 846 JJacquelin




The Solution Of The Differential Equation 1 Y X 2y Dx X



Http Fractal Math Unr Edu Ejolson 285 15 Extraprob Pdf
Resolver para x (x^2y^2)dx(x^2xy)dy=0 Factorizar la ecuación Toca para ver más pasos Factoriza a partir de Toca para ver más pasos Factoriza a partir de Dividir cada término por y simplificar Toca para ver más pasos Dividir cada término de por Reduce la expresión anulando los factores comunes Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeHow do I solve this differential equation y (y^22x^2) dxx (2y^2x^2) dy=0




15 2xy Y 2 Dx 2xy X 2 2x 2y 2 2xy 3 Dy 0 Homeworklib




Implicit Differentiation Advanced Example Video Khan Academy
The equation is also not separable The equation is also not homogenous, I don't think So what do I do?See the answer (2xy^22y)dx(2x^2y2x)dy=0 Expert Answer 100% (2 ratings) Previous question Next questionDifferential equation mathM(x,y) \, dx N(x,y) \, dy = 0 \tag*{}/math is nonexact when math\dfrac{\partial M}{\partial y} \ne \dfrac{\partial N}{\partial x




最新 Xy1 試す




Homogeneous Differential Equations
The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction y^ {2}2xyx^ {2}=0 y 2 2 x y x 2 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2x for b, and x^ {2} for c in the quadratic formula,Simple and best practice solution for y^2dx(x^2xy)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itAnswer to Solve the homogeneous equations x^2 dy ( y^2 xy) dx =0 By signing up, you'll get thousands of stepbystep solutions to your



Xy Y Y 2 2x 2xy Y Y 2 Y Dx X Dy 0 X 2 Chegg Com




Worked Example Implicit Differentiation Video Khan Academy
Math advanced math advanced math questions and answers Solve The DE (x^2yxyy)dx (x^2y2x^2)dy=0 The Solution Should Be Xlnxx^1y2lny=c` (x^(2)y^(2)) dx 2xy dy = 0`The ODE is homogeneous ODE of order one This is because the coefficients of dx and dy are both homogeneous two variables functions of the same order I suggest you write the ODE as y′ = 32t2t2−t−2 = f (t), (x = 0,t = y/x) Find the solution of (xy^22x^2y^3)dx (x^2yx^3y^2)dy=0
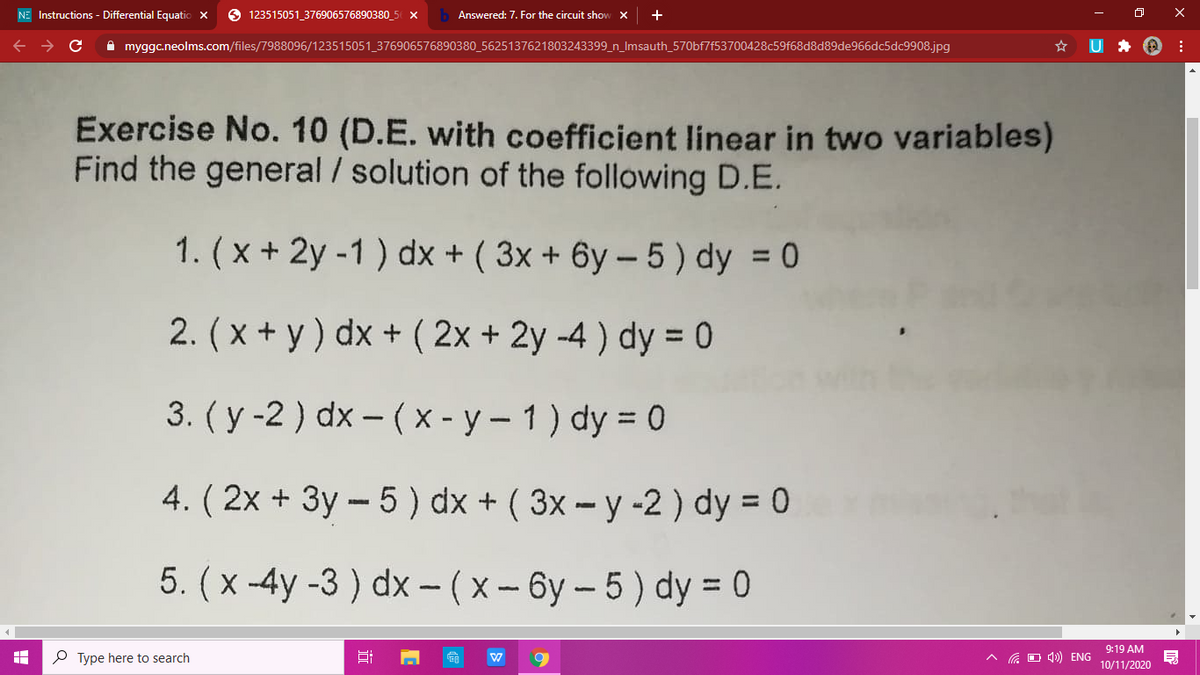



Answered X Y Dx 2x 2y 4 Dy 0 3d Bartleby



How To Solve This Differential Equation Y Xy 2 Dx X X 2 Y 2 Dy 0 Quora
Explanation x dy dx = 2x2y y, separating the variables 1 y dy dx = 2x2 1 x so dy y = 2x2dx dx x, integrating ∫ 1 y dy = ∫2x2dx ∫ 1 x dx, we have lny = x2 lnx C Which gives ln y x = x2 C eln y x = ex2c theory of logs ie, y x = ex2c and so,yHow do I solve (X*22xyy*2) dx (y*22xyx*2) dy=0? y^2 = x^2(2lnx c) We can rewrite this Ordinary Differential Equation in differential form (x^2 y^2) \ dx xy \ dy = 0 A as follows \ \ \ \ dy/dx = (x^2 y^2)/(xy) dy/dx = x/y y/x B Leading to a suggestion of a substitution of the form u = y/x iff y = ux And differentiating wrt x whilst applying the product rule dy/dx = u x(du)/dx Substituting into the




Solution Of Y Xy 1 Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange



What Is The Solution For Math Xy 2 2x 2y 3 Dx X 2y X 3y 2 Dy 0 Math Quora
Solution of the differential equation y(xy 2x2y2)dx x(xy x2y2)dy = 0 is given by (A) 2 logxlogy(1/xy)=C (B) 2 logylogx(1/xy)=C 2Equations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations (2x^2y)dx(x^2yx)dy=0 so that you understand betterIn order to complete the square, the equation must first be in the form x^ {2}bx=c Divide y, the coefficient of the x term, by 2 to get \frac {y} {2} Then add the square of \frac {y} {2} to both sides of the equation This step makes the left hand side of the equation a perfect square Square \frac {y




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q4 Pdf
1 Multiple by xayb so Mdx Ndy = 0 with M = xayb 1 xa 1yb 2, N = xa 1yb xa 2yb 1 xa 3yb 2 We choose a, b to achieve 0 = ∂yM − ∂xN = (b 1)xayb (b 2)xa 1yb 1 − (a 1)xayb − (a 2)xa 1yb 1 − (a 3)xa 2yb 2 = xayb((b − a)(1 xy) − (a 3)(xy)2) a = b = − 3 So 0 = Mdx Ndy = (x −Solution for (Xy^2x)dx (yx^2y)dy=0 equation Simplifying (X 1y 2 x) * dx (y 1x 2 y) * dy = 0 Reorder the terms for easier multiplication dx (X 1xy 2) (y 1x 2 y) * dy = 0 (X * dx 1xy 2 * dx) (y 1x 2 y) * dy = 0 (dxX 1dx 2 y 2) (y 1x 2 y) * dy = 0 Reorder the terms dxX 1dx 2 y 2 (1x 2 y y) * dy = 0 Reorder the terms for easier multiplication dxX 1dx 2 y 2 dy (1x 2 y y) = 0 dxX 1dx 2 y 2 (1x 2 y * dy y * dy) = 0 dxX 1dx 2 yThe differential equation xydx (x^2 2y^2)dy =0 can be rewritten as the following Bernulli equation, inthe unknown x(y) dx/dy x/y = 2y/x The equation can be turned to normal form taking x= V(y)^1/2 Obtain V' 2V/y = 4y The integrating factor is e^Integral of (–2dy/y) = e^(lny^2) = 1/y^2 Then, the solution for V(y) is




Y Xy 1 Dx X 1 Xy X 2 Y 2 Dy 0




X2 2xy Y2 Dx X Y 2dy 0 Brainly In
(xy^22x^2y^3)dx(x^2yx^3y^2)dy=0 (y2xy^2)dx=(x^2yx)dy y(12xy)dx=x(xy1)dy Substitute t=yx and t'=yxy' 3\int \frac {dx} x=\int \frac {(t1)dt} {t^2} This is an example of an exact DE — that is, it has the form F(x,y)dxG(x,y)dy=0, where \frac{\partial F}{\partial y}=\frac{\partial G}{\partial x} The solution to such a DE is givenSolution for (x^2y^2)dx (x^2xy)dy=0 equation Simplifying (x 2 y 2) * dx (x 2 1xy) * dy = 0 Reorder the terms for easier multiplication dx (x 2 y 2) (x 2 1xy) * dy = 0 (x 2 * dx y 2 * dx) (x 2 1xy) * dy = 0 Reorder the terms (dxy 2 dx 3) (x 2 1xy) * dy = 0 (dxy 2 dx 3) (x 2 1xy) * dy = 0 Reorder the terms dxy 2 dx 3 (1xy x 2) * dy = 0 Reorder the terms for easier multiplication dxy 2 dx 3 dy (1xy x 2) = 0 dxy 2 dx



Solve The Following Differential Equation E Xy Dy Dx Chegg Com



How To Solve This Differential Equation Y Y 2 2x 2 Dx X 2y 2 X 2 Dy 0 Quora



What Is The Solution Of Homogeneous Equation 2x Y Dx X 2y Dy 0 Quora



Www Math Tamu Edu Irinaholmes M308f M308f Hw3 Sol Pdf




Consider The Differential Equation Xy 2 Bx 2y Dx Chegg Com




Math 432 Hw 2 5 Solutions



How Is The Value In The Equation X 2 Y 3 Dx Ky 2x 1 Dy 0 Quora




Paper




最新 Xy1 試す




15 2xy Y 2 Dx 2xy X 2 2x 2y 2 2xy 3 Dy 0 Homeworklib




In Determine Whether The Given Differential Equation Chegg Com



Solve The Differential Equation Dy Dx X 2y 3 2x Y 3 Sarthaks Econnect Largest Online Education Community
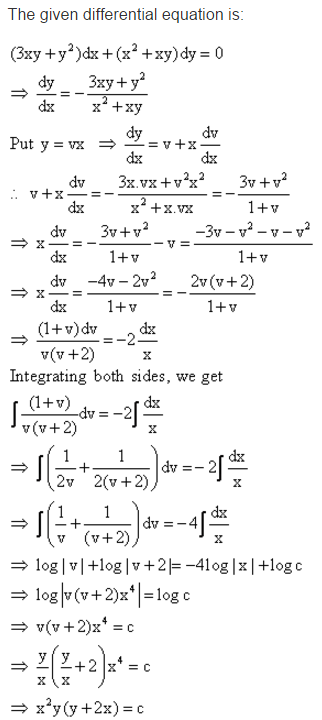



Find The Particular Solution Of Given Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 At X 1 Y 1 Mathematics Topperlearning Com D1ksg633




Ordinary Differential Equations



Www Ualberta Ca Csproat Homework Math 334 Assignment solutions Assignment 1 solutions Pdf




Differential Equations Solved Examples Show That Following Differential Equation Is Not Exact 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Then Find An Integrating Factor To Solve The Differential Equation




How To Solve Show The Differential Equations Are Exact 2xy Y Tany Dx X 2 X Tany 2 Secy 2 2 Dy 0 Te Tx 2x Dx Dt Xe Xt 0 Quora




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange



How To Solve The Differential Equation X X Y Dy Y 2dx 0 Quora




Find The General Solution Of The Differential Equation 2x 2 Y Dx X 2y X Dy 0 Study Com



Solve The Differential Equation Xy 2 X Dx X 2y Y Dy 0 Sarthaks Econnect Largest Online Education Community



Find The General Solution Of Y2dx X2 Xy Y2 Dy 0 Studyrankersonline




X 2 Y 2 Dx 2xy Dy 0 Integrating Factor Novocom Top



Search Q Implicit Differentiation Tbm Isch




Math 432 Hw 2 5 Solutions



Solve The Differential Equation Xy 2 Y 2 X Chegg Com



1




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When



What Is The General Solution Of The Differential Equation 2x 2y 3 Dy Dx X Y 1 Quora




Solve 3xy 2ay 2 Dx X 2 2axy Dy 0 Mathematics Stack Exchange




X 2 Y 2 Dx 2xy Dy 0 Integrating Factor Novocom Top




For Problems 26 Determine An Integrating Factor Chegg Com




Engineering Mathematics Notes




For Given Below Verify That The Given Function Implicit Or Explicit Is A Solution Of The Corresponding Differential Equation X 2 2y 2 Log Y X 2 Y 2 Dy Dx Xy 0 Mathematics Shaalaa Com




Dy Dx Xy 2y X 2 Xy 3y X 3 Variables Separables Alexander Estrada Youtube
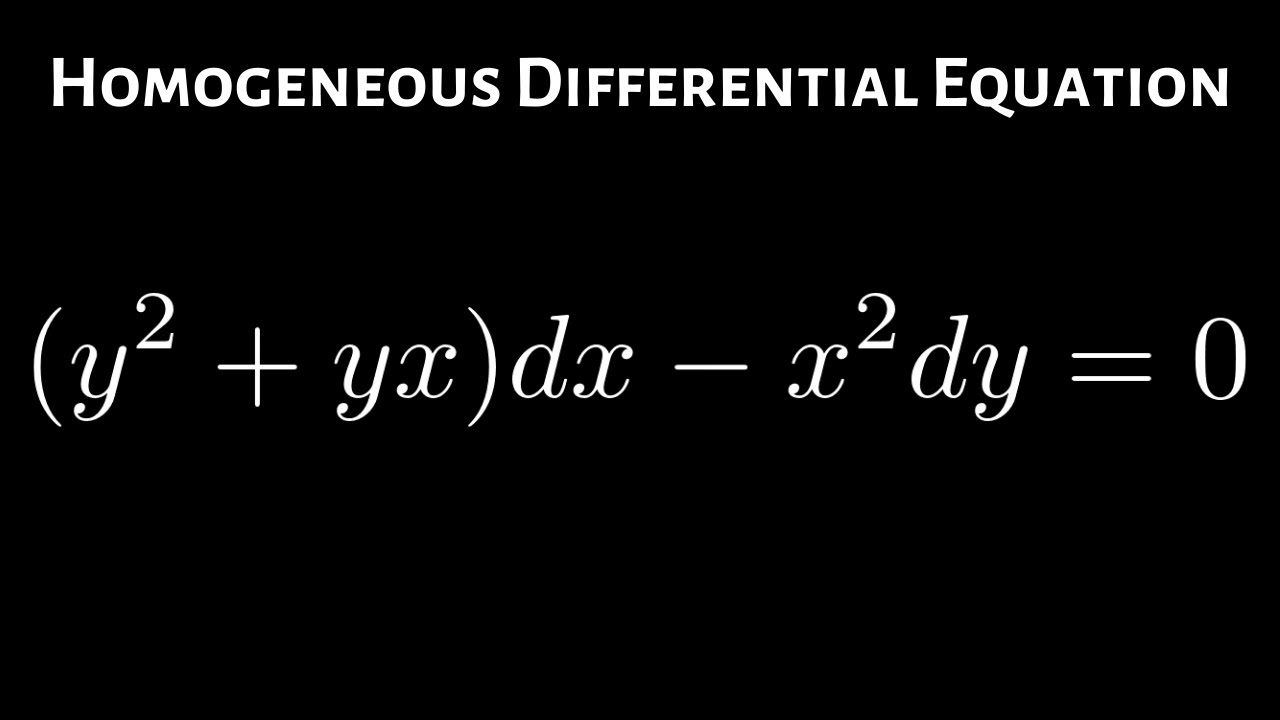



Homogeneous Differential Equation Y 2 Yx Dx X 2dy 0 Youtube




Engineering Mathematics Notes




Ejercicios Propuestos Ecuaciones Diferenciales Primer Orden Pdf Differential Equations Equations




Ex 9 5 5 Show Homogeneous X2 Dy Dx X2 2y2 Xy Ex 9 5
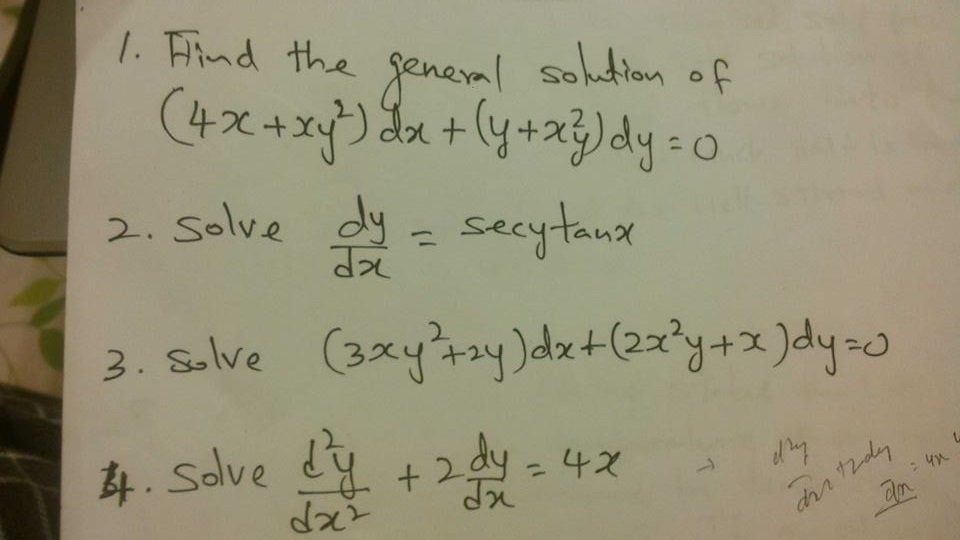



1 Find The General Solution Of 4x Xy 2 Dx Y Chegg Com




Y Xy 2x Y Dx X Xy X Y Dy 0 Brainly In




Example 21 Find General Solution Ydx X 2y2 Dy 0




Math 432 Hw 2 5 Solutions Pdf Free Download




Differential Equatio Long Answer Questions 7 M R Solye 2x Y 3 Dx 2y X 1 Dy Sol Dy 2x Y 3 Given Equation Is




Engineering Mathematics Notes




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange




Engineering Mathematics Notes




Lesson 6 Exact Equations Determine Whether Or Not Each Of




Solve The Following Differential Equations I Y 2 D X Left X Y X 2 Right D Y 0 Ii X 2 Y D X Left X 3 Y 3 Right D Y 0 Iii Frac D Y D X Tan Left Frac Y X Right Frac Y X Iii Frac D Y D X Frac X 2 Y 2 X Y 0 Iv
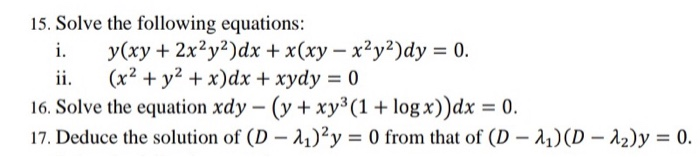



15 Solve The Following Equations I Y Xy 2x2y2 Dx Chegg Com



Www Tau Ac Il Levant Ode Solution 6 Pdf
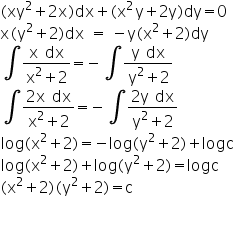



Xy 2 2x Dx X 2y 2y Dy 0 Mathematics Topperlearning Com X0ufmuww




Example 17 Show 2y E X Y Dx Y 2x Ex Y Dy 0 Particular




Solve The Following Differential Equations 1 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Youtube
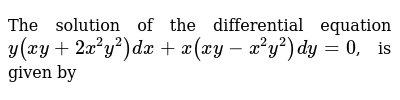



The Solution Of The Differential Equation Y Xy 2x 2y 2 Dx




The Solution Of The Differential Equation Y Xy 2x 2y 2 Dx X Xy X 2y 2 Dy 0 Is Given Youtube



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf



Www Ualberta Ca Csproat Homework Math 334 Assignment solutions Assignment 2 solutions Pdf



What Is The General Solution Of The Differential Equation 2x 2y 3 Dy Dx X Y 1 Quora



1



Solved Solving Exact First Oder Differential Equations 2xydx X 2 Cosy Dy 0 Y Xy 2 1 1 X 2y 2x Y Dx X 3y Dy 0 2x Y 4 Dx X 3y 12 Dy 0 Ye X S Course Hero
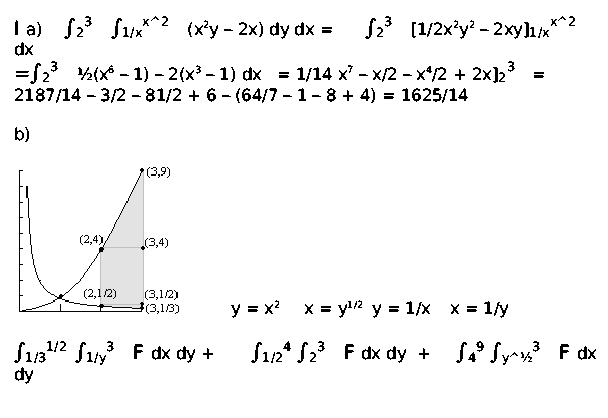



Answers To The Review Problems For The First Exam 251 05 10 In Spring 06




How To Solve 3xy Y 2 Dx X 2 Xy Dy 0 Also I Wish To Knw When To Use Y Vx Or X Vy Mathematics Topperlearning Com H9faf2xx




Solution Of The Differential Equation Y Xy 2x 2y 2 Dx X Xy X 2y 2 Dy 0 Is Given By P Log X Q Log Y 1 Xy C



Solved Solving Exact First Oder Differential Equations 2xydx X 2 Cosy Dy 0 Y Xy 2 1 1 X 2y 2x Y Dx X 3y Dy 0 2x Y 4 Dx X 3y 12 Dy 0 Ye X S Course Hero



Solve Xy 3 Y Dx 2 X 2y 2 X Y 4 Dy 0 Youtube



What Is The Solution For Math Xy 2 2x 2y 3 Dx X 2y X 3y 2 Dy 0 Math Quora




Differential Equations Solved Examples Show That Following Differential Equation Is Not Exact 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Then Find An Integrating Factor To Solve The Differential Equation



Search Q D Dx Formula Tbm Isch




First Order Differential Equations Ppt Download



Solved Solve The Following Differential Equations X Y 3 Dx X Y 1 Dy 0 2 X Y 1 Dx 3x 4y 2 Dy C 3 1 Y 2 Xy 2 Dx X 2y Y 2xy Dy Course Hero



Solve Xy 3 Y Dx 2 X 2y 2 X Y 4 Dy 0 Youtube



Find The Particular Solution Of The Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 For X 1 Y 1 Sarthaks Econnect Largest Online Education Community




Solve Y 1 Xy Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange




In Exercises 1 17 Determine Which Equations Are Exact Chegg Com




Show That The Equation 5x4 3x2y2 2xy3 Dx 2x3y 3xy2 5y4 Dy 0 Is An Exact Differential Equation Find Its Solution Mathematics 2 Question Answer Collection



How To Solve This Differential Equation Y Y 2 2x 2 Dx X 2y 2 X 2 Dy 0 Quora




X Y 2 Dx X 2y 3 Dy 0 Brainly In




The Solution Of The Differential Equation Y Xy 2x 2y 2 Dx



Http Pages Mtu Edu Struther Courses Old Other Older 3521 10 Quizstuff Fromgil Ch 2 Pdf



0 件のコメント:
コメントを投稿